Diagram conventions
Notice that the way we indexed cells on the previous page is the same way as we index entries in matrices, first by rows and then by columns. This way of doing things is called English notation and is the most commonly used in the literature.
Let $\lambda = (6,3,1)$. We highlight the cells $s = (1,3), t = (2,3) \in \mathrm{Young}(\lambda)$ in English notation below:
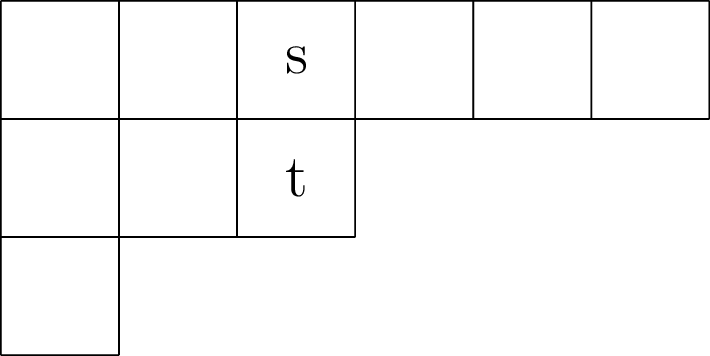
We will introduce three other ways to draw Young diagrams: French notation, Russian notation, and Cartesian notation, and draw the Young diagram of $\lambda = (6,3,1)$ with the cells $s = (1,3), t = (2,3) \in \mathrm{Young}(\lambda)$ highlighted below using each of these conventions in turn.
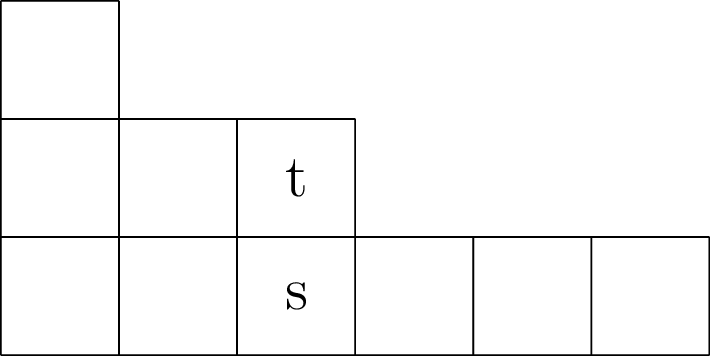
French notation
French notation relates to English notation by a reflection in the $x$-axis, i.e. stack parts in rows with index increasing from bottom to top, i.e. longest row/largest part at the bottom, aligned to the bottom-left corner of the 1st quadrant.
Russian notation
Russian notation may be obtained by rotating a diagram drawn using English notation anticlockwise 135 degrees.
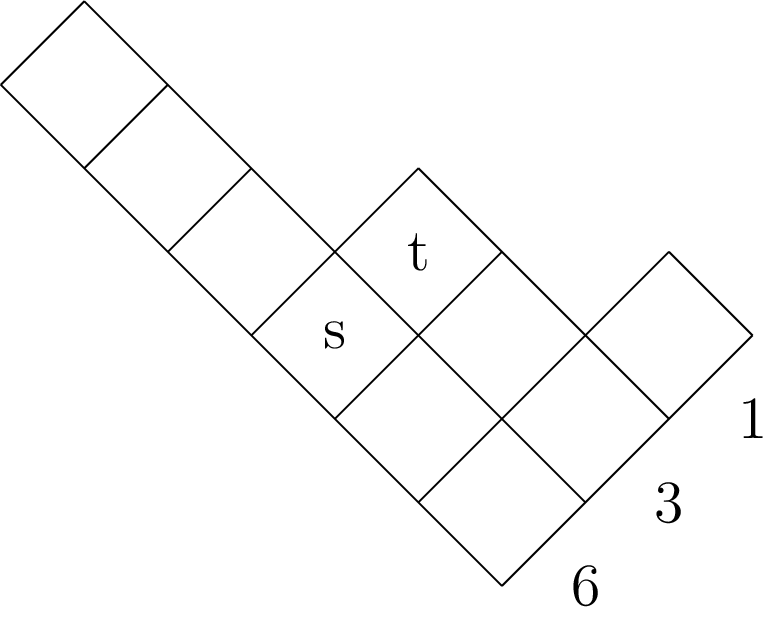
Diagrams in Russian notation will be used to motivate Maya diagrams later.
Cartesian notation
Sometimes we will use a convention obtained by rotating a diagram drawn using English notation anticlockwise 90 degrees, which we will call ‘Cartesian’ notation. In Cartesian notation the diagrams are aligned to the bottom-left corner of the 1st quadrant, and parts correspond to columns which decrease in size from left to right. The $(i,j)$ coordinates for cells resemble the standard Cartesian coordinates $(x,y)$ for the Euclidean plane.
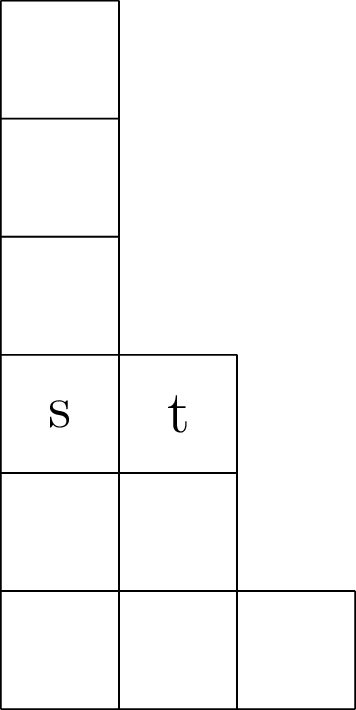
We will revisit Cartesian notation when we discuss applications to monomial ideals in algebraic geometry.
Summary
In the table below we summarize the relations between the different conventions for drawing Young diagrams and indexing cells in terms of the change of basis matrix to the standard Euclidean basis:
| Convention | Transformation matrix |
|---|---|
| Cartesian | $\left(\begin{array}{cc}1 & 0\\0 & 1\end{array}\right)$ |
| English | $\left(\begin{array}{cc}0 & 1\\-1 & 0\end{array}\right)$ |
| French | $\left(\begin{array}{cc}0 & 1\\1 & 0\end{array}\right)$ |
| Russian | $\left(\begin{array}{cc}1 & -1\\1 & 1\end{array}\right)$ |
Display options in SageMath
We can choose how we want Ferrers and Young diagrams/tableaux to be displayed in SageMath using Partitions.options() to set global options. The keyword convention (or its alias notation) can be set to either 'French' or 'English' (not case sensitive), and we can also use the diagram_str keyword to choose the character used for cells when printing Ferrers diagrams. By default, Ferrers diagrams are printed using the English convention with asterisks "*" for cells.
mu = Partition([5,5,3,2,1])
mu.pp()
# *****
# *****
# ***
# **
# *
Partitions.options(convention='French', diagram_str="&")
mu.pp()
# &
# &&
# &&&
# &&&&&
# &&&&&
Partitions.options._reset()
You can practice executing SageMath and Python code in the SageMathCell below.