Sample Mathematics Aptitude Test

This page will contain selected solutions to exercises from the Sample Mathematics Aptitude Test found online here.

Table of Contents

Short Questions

SQ1. Digital clock displays

Consider a 12 hour digital clock (one that takes values from 00:00 to 11:59). Look at it at a random point during a 12 hour period.

SQ1 Solution

All 720 possible clock displays can be expressed in the form $hh$:$m_{1}m_{2}$, where $hh$ denotes the hour display, ranging from $00$ to $11$, and $m_{1}m_{2}$ represents the minute display, with the $m_{1}$ digit ranging from $0$ to $5$ and $m_{2}$ ranging from $0$ to $9$.

Sampling a clock display at random can be split into independently sampling values of $hh$, $m_{1}$, and $m_{2}$ uniformly from their possible values.

To calculate the probability of at least one ‘1’ digit on the clock display, we take the complement of the probability of seeing no ‘1’ digits on the clock display. $$ P(\text{at least one digit is ‘1’}) = 1 - P(\text{no digits are ‘1’}) $$ Then, by independence, we have $$ P(\text{no digits are ‘1’}) = P(hh \not\in \{ 01, 10, 11 \})P(m_{1} \neq 1)P(m_{2} \neq 1) = \frac{9}{12} \times \frac{5}{6} \times \frac{9}{10} = \frac{9}{16} $$ Therefore, $$P(\text{at least one digit is ‘1’}) = 1 - \frac{9}{16} = \frac{7}{16}$$ Next, to calculate the probability of exactly one ‘1’ digit on the clock display we split this into the mutually exclusive cases depending on where the single ‘1’ digit appears, either in the value of $hh$, $m_{1}$, or $m_{2}$. This yields $$ \begin{split} P(\text{exactly one digit is ‘1’}) & = P(hh \in \{ 01, 10 \})P(m_{1} \neq 1)P(m_{2} \neq 1) \\
& + P(hh \not\in \{ 01, 10, 11 \})P(m_{1} = 1)P(m_{2} \neq 1) \\
& + P(hh \not\in \{ 01, 10, 11 \})P(m_{1} \neq 1)P(m_{2} = 1) \\
& = \frac{2}{12} \cdot \frac{5}{6} \cdot \frac{9}{10} + \frac{9}{12} \cdot \frac{1}{6} \cdot \frac{9}{10} + \frac{9}{12} \cdot \frac{5}{6} \cdot \frac{1}{10} \\
& = \frac{3}{10} \end{split} $$

Therefore, when randomly sampling from the display of a 12 hour digital clock taking values from 00:00 to 11:59, one would expect to see at least one digit taking the value ‘1’ on the display $43.75\%$ of the time, and one would expect to see exactly one digit taking the value ‘1’ on the display $30\%$ of the time.

Tags: Probability

Related reading:

SQ2. Prime factors and greatest common divisors

Let $a, b$ be positive integers and let $p$ be a prime factor of $a^{b} − 1$. Show that either $\gcd(p, a − 1)$ or $\gcd(b, p − 1)$ must be greater that $1$.

SQ2 Solution

First, recall two important facts that we will use in the proof: Fermat’s Little Theorem and Bézout’s identity. We will also draw on ideas from elementary group theory, in particular the notion of the order of a group element, and properties of $\mathbb{Z}/p\mathbb{Z}$.

By the assumption that $p$ divides $a^{b} − 1$ it follows that $p$ does not divide $a$. Otherwise, $p$ would divide both $a^{b}$ and $a^{b} − 1$ and hence also their difference $a^{b} - (a^{b} − 1) = 1$, but $1$ does not have any prime divisors, so $p$ cannot divide $a$.

Note that since $p$ is prime, $\gcd(p, a − 1)$ is greater than $1$ if and only if $\gcd(p, a − 1) = p$, or equivalently, if and only if $p$ divides $a - 1$.

Case 1. Suppose $\gcd(p, a − 1) = 1$, so $p$ does not divide $a - 1$. We will show that we must have $\gcd(b, p − 1) > 1$. By our main assumption, $a^{b} \equiv 1 \ (\mathrm{mod}\ p)$. As $p$ does not divide $a$, we may apply Fermat’s Little Theorem to deduce that $a^{p - 1} \equiv 1 \ (\mathrm{mod}\ p)$. It follows that the (multiplicative) order of $a$ in $\left( \mathbb{Z}/ p \mathbb{Z} \right)^{\times}$ is a common factor of $b$ and $p - 1$, so $\mathrm{order}(a) \le \gcd(b, p − 1)$. As we assume $p$ does not divide $a - 1$, we have $a \not\equiv 1 \ (\mathrm{mod}\ p)$, and in particular $\mathrm{order}(a) > 1$. Hence, $$\gcd(b, p − 1) \ge \mathrm{order}(a) > 1$$ as required.

Case 2. Now, suppose $\gcd(b, p − 1) = 1$. We will show that $p$ divides $a - 1$ and hence $\gcd(p, a − 1) = p > 1$. By Bézout’s identity, there exist integers $x, y$ such that $bx + (p - 1)y = \gcd(b, p − 1) = 1$. Then $$a = a^{1} = a^{bx + (p - 1)y} = (a^{b})^{x}(a^{p - 1})^{y} \equiv 1^{x}1^{y} = 1 \ (\mathrm{mod}\ p)$$ once again using that $a^{b} \equiv 1 \ (\mathrm{mod}\ p)$, and $a^{p - 1} \equiv 1 \ (\mathrm{mod}\ p)$ by Fermat’s Little Theorem.
Hence $a - 1$ is divisible by $p$ as required.

Tags: Modular arithmetic, Number theory, Group theory

SQ3. Estimating coin bias

Alice and Bob are given a set of five biased coins. They both estimate the probability that each coin will show a head when flipped, and each coin is then flipped once. These are the estimates and values observed:

Coin Alice’s estimates Bob’s estimates Observed
1 0.4 0.2 Heads
2 0.7 0.8 Heads
3 0.2 0.3 Tails
4 0.9 0.6 Tails
5 0.4 0.3 Heads

Whom would you say is better at estimating the bias of the coins, and why?

SQ3 Solution

By coding “Heads” as 1 and “Tails” as 0, we can calculate the (absolute) error and the squared error for each estimate and sum these errors over the five coins. The results are shown in the table below.

Coin Alice’s estimates Bob’s estimates Observed Is “Heads”? $\mathrm{Err}(A)$ $\mathrm{Err}(B)$ $\mathrm{Err}(A)^{2}$ $\mathrm{Err}(B)^{2}$
1 0.4 0.2 Heads 1 0.6 0.8 0.36 0.64
2 0.7 0.8 Heads 1 0.3 0.2 0.09 0.04
3 0.2 0.3 Tails 0 0.2 0.3 0.04 0.09
4 0.9 0.6 Tails 0 0.9 0.6 0.81 0.36
5 0.4 0.3 Heads 1 0.6 0.7 0.36 0.49
Total 2.6 2.6 1.66 1.62

We can see from the table of results that, in terms of absolute error both Alice and Bob are equally bad at predicting the outcome of the coin flip, where their coin bias estimate is used as a proxy for the most likely outcome of a single flip. However, when comparing the sum of squared errors, which will more heavily penalize overconfidence in an incorrect outcome, we find that Bob is marginally better than Alice at predicting the outcome of the coin flips (and hence estimating the bias of the coins?).

SQ3 Discussion

It should be noted that both Alice and Bob performed slightly worse than a totally naive prior estimate of a $0.5$ probability of landing on heads for each coin, which might cast doubts on their predictive skills if the experiment was more powerful. One might also like to examine the level of statistical correlation between the predictions and the outcomes, in case one’s predictions are systematically wrong which could be helpful in this binary case/for excluding an unlikely outcome.

It could be said that a single flip each of five independent biased coins is not particularly strong evidence for determining forecasting skills. To test one’s ability to predict the bias of a coin (from, say, physical examination beforehand) it would make sense to perform multiple flips of each biased coin so that an observed estimate $\text{Heads} / \text{Flips}$ of the bias could be compared to the predictor’s estimate. Testing more predictions by flipping a larger set of coins would also increase the information gained from the experiment.

A more rigorous analysis from the viewpoint of information theory or Bayesian statistics might yield more insight into this scenario. This scenario can also be related to examining the predictive power of a binary classifier in machine learning.

This mean squared error for forecasts is actually more commonly known as the Brier score, whose definition extends to mutually exclusive multi-category forecasts. This article, written by Paul J. H. Schoemaker and Philip E. Tetlock for the Harvard Business Review, explains the benefits of better organisational decision making for businesses and suggests general methods to achieve them, introducing the Brier score as a way to measure forecasting skills, whilst emphasising the importance of carefully tracking the analysis process used to make predictions so that they can be improved where possible through trial and error. Techniques for reducing cognitive biases, and producing forecasts in teams was also shown to produce better results. For more information on The Good Judgement Project, the study on which the above article is based, see also the 2015 book by Philip E. Tetlock and Dan Gardner, Superforecasting: The Art and Science of Prediction.

Shortcomings of the Brier score when it comes to differential penalization for false-positive and false-negative misclassifications (as opposed to an overall measure of forecasting accuracy), which may be relevant in clinical scenarios where making a correct or incorrect prediction come with different levels of utility, are addressed in the following article. The authors of this article recommend an alternative method for comparing clinical diagnostic tests or prediction models called net benefit. Limitations in comparing forecasting performance on very rare events are also discussed on the Wikipedia page for Brier score. Related reading on the sensitivity/recall (true positive rate) and specificity (true negative rate) and other metrics for judging binary classification prediction models can be found here and here.

Tags: Forecasting, Statistics, Information theory, Machine Learning

References:

Related Reading:

SQ4. A devilish question

Find an example of a function $f$ from $[0, 1]$ to $[0, 1]$ with the following properties:

  1. $f$ is continuous;
  2. $f(0) = 0$;
  3. $f(1) = 1$;
  4. $f(x)$ is locally constant almost everywhere.

SQ4 Solution

Whether you can answer this question without the aid of the internet may depend on how well/how recently you remember your second year undergraduate calculus/analysis course. An example of such a function is the Cantor function which “is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure.”

Devil’s staircase

The definition of the Cantor function by iterative construction makes clear that the function has the desired properties, in particular it is continuous as the uniform limit of a sequence of continuous functions. More interesting information about the related Cantor set is also available online.

Tags: Analysis, Measure theory, point-set topology

SQ5. A piece of cake

You have a large rectangular cake, and someone cuts out a smaller rectangular piece from the middle of the cake at a random size, angle and position in the cake (see the picture below). Without knowing the dimensions of either rectangle, using one straight (vertical) cut, how can you cut the cake into two pieces of equal area?

Your browser does not support the HTML5 canvas tag.

SQ5 Solution

For a while I was confused about the ‘vertical’ restriction on the straight cut when looking at this picture, but seeing it as the cross section when viewed from above I realised that ‘vertical’ refers to the hidden $z$-axis of the cake rather than the $y$-axis of the cross section in the image. This is to avoid slicing the cake horizontally into top and bottom pieces of equal area, which would be inappropriate for a cake with icing.

Any straight line through the midpoint of a rectangle will cut it into two pieces of equal area regardless of the angle of the line. Therefore it suffices to cut along the (unique) line passing through both the midpoint of the original cake rectangle and the midpoint of the rectangular shaped hole left by the removed piece of cake.

The solution to this question is satisfying to think about, and probably worth trying for yourself at home so you can have your cake and eat it too.

Your browser does not support the HTML5 canvas tag.

Tags: Geometry

SQ6. Random number generation

A random number generator produces independent random variates $x_{0}, x_{1}, x_{2}, \ldots$ drawn uniformly from $[0, 1]$, stopping at the first $x_{T}$ that is strictly less than $x_{0}$. Prove that the expected value of $T$ is infinite. Suggest, with a brief explanation, a plausible value of $P(T = \infty)$ for a real-world (pseudo-)random number generator implemented on a computer.

SQ6 Solution

We first consider the expected stopping time conditional on the value of $x_{0}$, i.e. the expected value of $T$ given that $x_{0} = p$ for some $p \in [0, 1]$. Once we have a formula for $\mathbb{E}[T | x_{0} = p]$, we may integrate to find $$\mathbb{E}[T] = \int_{0}^{1} \mathbb{E}[T | x_{0} = p] dp$$ as $x_{0}$ is uniformly distributed on $[0, 1]$.

We may calculate $\mathbb{E}[T | x_{0} = p]$ in two different ways: The first is to consider the probability of stopping at a given time $T$, which occurs when $x_{T} < x_{0}$ and $x_{i} \ge x_{0}$ for $i = 1, \ldots, T - 1$, and using this in the definition of expectation: $$ \mathbb{E}[T | x_{0} = p] = \sum_{t = 1}^{\infty} t P(T = t | x_{0} = p) = \sum_{t = 1}^{\infty} t P(x_{T} < p) \prod_{i = 1}^{t - 1} P(x_{i} \ge p) = \sum_{t = 1}^{\infty} t p (1 - p)^{t - 1} $$ The right hand side is a special case of an Arithmetico–geometric sequence, for which Swain has a wonderful picture proof (originally published in Mathematics Magazine in 1994, and reproduced on the Wolfram Mathworld website here) demonstrating the formula $$\sum_{k=1}^{\infty} k r^{k} = r + 2r^{2} + 3r^{3} + \ldots = \frac{r}{(1 - r)^{2}} \text{ for } 0 \le r < 1.$$ 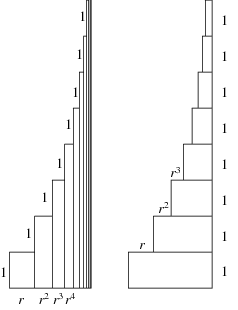Gabriel’s Staircase The picture proof proceeds by computing the same area in two different ways, applying the trick for deriving the formula of a geometric series: If $S_{n} = \sum_{k=1}^{n-1} r^{k-1} = 1 + r + r^{2} + \ldots + r^{n - 1}$, then $(1 - r) S_{n} = 1 - r^{n}$, so $S_{n} = \frac{1 - r^{n}}{1 - r}$ and $\sum_{k=1}^{\infty} r^{k-1} = \lim_{n \to \infty} S_{n} = \frac{1}{1 - r}$ for $0 \le r < 1$. This summation trick is applied twice, first in calculating the area of each horizontal row, and then in summing up over all rows after taking out a common factor.

We apply the formula to our summation to find that $$\mathbb{E}[T | x_{0} = p] = \sum_{t = 1}^{\infty} t p (1 - p)^{t - 1} = \frac{1}{p}.$$

Alternatively, we may analyse the problem from the perspective of the hitting time of an Absorbing Markov Chain. The $x_{1}, x_{2}, \ldots$ are independent uniform random variates, so the process of successively sampling $x_{i}$, stopping when $x_{i} < x_{0}$, is memoryless.

We may equivalently formulate the problem as flipping a biased coin with fixed probability $p$ of landing on heads, and calculating the expected number of coin tosses before observing the coin landing on heads; coin flips are not affected by previous (or future) coin flips.

Let $T_{i}$ denote the number of remaining draws before stopping after already drawing $x_{0}, \ldots, x_{i}$. By the memorylessness property, if the first coin flip lands on tails (i.e. if $x_{1} \ge x_{0}$), then expected remaining number of flips afterwards has not changed compared to before making the flip, so $\mathbb{E}[T_{1} | x_{1} \ge x_{0}, x_{0} = p] = \mathbb{E}[T_{0} | x_{0} = p]$.

Following this line of reasoning when considering all possible outcomes of drawing $x_{1}$, we deduce that: $$ \mathbb{E}[T_{0} | x_{0} = p] = 1 + \mathbb{E}[T_{1} | x_{1} < x_{0}, x_{0} = p] P(x_{1} < p) + \mathbb{E}[T_{1} | x_{1} \ge x_{0}, x_{0} = p] P(x_{1} \ge p) $$ $$ = 1 + 0 \cdot p + \mathbb{E}[T_{1} | x_{1} \ge x_{0}, x_{0} = p] (1 - p) = 1 + (1 - p) \mathbb{E}[T_{0} | x_{0} = p] $$ Rearranging this equation once again yields the result: $\mathbb{E}[T_{0} | x_{0} = p] = \frac{1}{p}$.

Now that we know the expected stopping time conditional on the value of $x_{0}$, we can integrate over all the possible values of $x_{0}$, uniformly weighted, to find that $$\mathbb{E}[T] = \int_{0}^{1} \mathbb{E}[T | x_{0} = p] dp = \int_{0}^{1} \frac{1}{p} dp$$ which diverges to infinity, and so we have shown that the expected value of $T$ is infinite, as required.

When dealing with a real-world (pseudo-)random number generator implemented on a computer, the number of possible values for the $x_{i}$ is finite, and a good implementation will give a roughly uniform distribution among a (large) discrete set of values in the interval $[0, 1]$. Therefore, a plausible value for $P(T = \infty)$ is $P(x_{0} = 0)$, in which case we can be certain the process will not stop. The actual value of $P(x_{0} = 0)$ may depend on the kind of (pseudo-)random number generator used and possibly on incidences of numerical underflow, but can be reasonably approximated by the reciprocal of the number of distinct (pseudo-)random values that can be generated. For a simple example of a pseudo-random number generator based on modular arithmetic and an affine linear transform, see here.

SQ6 Aside

More pictorial proofs regarding ‘staircase series’ can be found in another Mathematics Magazine article published in 2018, whilst an excellent collection of other proofs without words can be found at the Art of Problem Solving online wiki, including a proof of the formula for infinite geometric series using similar triangles. Wolfram Alpha also has references to more pictorial proofs here.

Geometric series and similar triangles

Finding succinct expressions for certain power series expressions also occurs in the study of generating functions, with applications in number theory, combinatorics, and beyond.

Tags: Probability, Markov Chains, Random number generators

References:

Related Reading:

SQ7. Four digit square numbers

Prove that there does not exist a four-digit square number $n$ such that $n \equiv 1 \ (\mathrm{mod}\ 101)$.

SQ7 Solution

Noting that $31^{2} = 961, 32^{2} = 1024, 99^{2} = 9801, 100^{2} = 10000$, we find that the set of four digit square numbers is precisely $\{ n = x^{2} : x = 32, \ldots, 99 \}$. Suppose, for contradiction, that we have a four digit square number $n = x^{2}$ such that $n \equiv 1 \ (\mathrm{mod}\ 101)$. This means that there is an integer $k$ such that $n - 1 = x^{2} - 1 = 101k$. By factorising the difference of two squares we find that $(x + 1)(x - 1)$ is divisible by $101$. As $101$ is prime, it follows that either $(x + 1)$ or $(x - 1)$ is divisible by $101$, however this is impossible for $x \in \{ 32, \ldots, 99 \}$. Therefore, there can be no four-digit square number which is congruent to $1$ modulo $101$, as required.

Tags: Modular arithmetic, Number theory

SQ8. Scaled Fourier transform

The Fourier transform of a function $f(t)$ is defined as: $$F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-2 \pi i \omega t} dt.$$ Express the Fourier transform of $f(\alpha t)$ in terms of $F$, $\alpha$ and $\omega$.

SQ8 Solution

The Fourier transform of $f(\alpha t)$ is $\int_{-\infty}^{\infty} f(\alpha t) e^{-2 \pi i \omega t} dt$. When $\alpha \neq 0$, we can use the substitution $s = \alpha t$, so that $t = \frac{s}{\alpha}$ and $dt = \frac{1}{\alpha} ds$. In the case when $\alpha > 0$, the limits of integration are preserved and we get $$\int_{-\infty}^{\infty} f(\alpha t) e^{-2 \pi i \omega t} dt = \frac{1}{\alpha} \int_{-\infty}^{\infty} f(s) e^{-2 \pi i (\frac{\omega}{\alpha}) s} ds = \frac{1}{\alpha} F(\frac{\omega}{\alpha})$$ In the case that $\alpha < 0$, the limits of integration are reversed and we get $$\int_{-\infty}^{\infty} f(\alpha t) e^{-2 \pi i \omega t} dt = -\frac{1}{\alpha} \int_{-\infty}^{\infty} f(s) e^{-2 \pi i (\frac{\omega}{\alpha}) s} ds = -\frac{1}{\alpha} F(\frac{\omega}{\alpha})$$ Combining these two, we find that for $\alpha \neq 0$ the Fourier transform of $f(\alpha t)$ is given by $\frac{1}{\lvert \alpha \rvert} F(\frac{\omega}{\alpha})$.

When $\alpha = 0$, $f(\alpha t) = f(0)$ is constant with respect to $t$ and we have $$\int_{-\infty}^{\infty} f(\alpha t) e^{-2 \pi i \omega t} dt = f(0) \int_{-\infty}^{\infty} e^{-2 \pi i \omega t} dt = f(0) \delta(\omega)$$ a multiple of the Dirac delta function. This requires more sophisticated analysis than simple techniques for evaluating improper integrals. See here for more properties of the Fourier transform.

Tags: Fourier transform, Calculus, Improper integration

SQ9. Intersection of multisets

A multiset is a collection of objects, some of which may be repeated. So, for example, $\{ 1, 3, 5, 3, 2, 7, 2 \}$ is a multiset. The multiplicity of an element in a multiset is the number of times that element occurs in the multiset. Intersections of multisets can be produced as follows: given multisets $A$ and $B$, the multiplicity of an element in $A \cap B$ is the minimum of its multiplicities in each of $A$ and $B$. Given multisets $A$ and $B$, with unordered elements, outline an algorithm for generating the intersection $A \cap B$.

SQ9 Solution

Initially modelling a multiset with unordered elements as an unsorted list or array, we outline three different algorithms for computing the intersection of two unordered multisets and discuss their time complexity. Further optimizations for the methods described (as well as alternative solutions) exist. Define the size of a multiset to be the total number of elements it contains or equivalently the sum of the multiplicities of its distinct elements, and let the size of multisets $A$ and $B$ be $a$ and $b$, respectively. The space complexity of the result $A \cap B$ is simply the size $|A \cap B|$ of the intersection, which is bounded above by $\min(a, b)$.

  1. Create a list data structure to hold the result of the intersection of $A$ and $B$.
  2. For each element in $A$ (sequentially), check whether it occurs in $B$ (sequential/linear search);
    • If so, add this element once to the list of common elements and remove it once from $B$ (e.g. remove the first occurence in $B$);
    • If not, move on to the next element in $A$;
  3. Once the loop is completed, the resulting list will contain all of the common elements with the appropriate multiplicities.

The time complexity of this algorithm is $O(ab)$ since we loop over the $a$ elements of $A$, and for each loop we sequentially/linearly search through the list $B$, which has runtime $O(b)$. The worst case behaviour is typically achieved when the two multisets are disjoint/do not intersect.

def intersection_sequential(A: list, B: list) -> list:
    result = []
    for x in A:
        if (len(B) == 0): break; # Stop if `B` is empty
        if (x in B): # Sequential/linear search for `x` in unsorted list `B`
            result.append(x) # Add the common element `x` to `result` once
            B.remove(x) # Remove the first occurence of `x` from `B` (once)
    return result
  1. Create a list data structure to hold the result of the intersection of $A$ and $B$.
  2. Sort the list $B$ (assumes a (total) ordering on the elements of the multisets, such as for numbers or strings).
  3. For each element in $A$ (sequentially), check whether it occurs in $B$ using a binary search;
    • If so, add this element once to the list of common elements and remove it once from $B$ (e.g. remove the first occurence in $B$);
    • If not, move on to the next element in $A$;
  4. Once the loop is completed, the resulting list will contain all of the common elements with the appropriate multiplicities.

The runtime for sorting $B$ is $O(b \log b)$, then we loop over the $a$ elements of $A$, for which each binary search through the sorted list $B$ has runtime $O(\log b)$. Therefore the overall runtime is $O((a + b) \log b)$. This method is asymptotically faster than method 1, but makes the (possibly incorrect) assumption that all elements in the multisets can be compared using the operators < and > rather than only ==. If this is the case, further optimizations may be achieved by choosing which multiset out of $A$ and $B$ to sort (or both, with further modifications to the algorithm) contingent on comparing the size of $A$ and $B$.

def intersection_with_sort(A: list, B: list) -> list:
    result = []
    B.sort() # Sort `B` in place
    for x in A:
        if (len(B) == 0): break; # Stop if `B` is empty
        if (x < B[0] or x > B[-1]): continue; # Skip if x < min(B) or x > max(B) to save time
        if (x in B): # Binary search for `x` in sorted list `B`
            result.append(x) # Add the common element `x` to `result` once
            B.remove(x) # Remove the first occurence of `x` from `B` (once)
    return result
Method 3. Hash table

For this method, we remodel a multiset using a hash table, where the keys are the distinct elements and the values are their respective multiplicities. This requires the elements of a multiset to be hashable.

  1. Create empty hash table/dictionary data structures A_dict, B_dict, and result to hold the data for $A$, $B$, and $A \cap B$, respectively.
  2. Calculate the multiplicities of the elements in $A$ by counting. For each element $x$ in $A$, check whether it is already a key in A_dict;
    • If so, increment the value at A_dict[x] by one;
    • Otherwise, add the key-value pair (x, 1) to A_dict;
  3. Repeat this process for $B$ to populate B_dict with element counts/multiplicities.
  4. For each distinct element in $A$, check whether it occurs in $B$ using the hash table lookup;
    • If so, add a new entry to the results table with the common element as the key and the minimum of its multiplicities in each of $A$ and $B$ as the value;
    • If not, move on to the next (distinct) element in $A$;
  5. Once the loop is completed, the resulting table will contain all of the common elements as keys with their multiplicities in $A \cap B$ as the corresponding values.

In a well-implemented hash table the average runtime for each lookup is constant time $O(1)$, i.e. independent of the number of elements stored in the table. Such designs also allow arbitrary insertions and deletions of key-value pairs, at (amortized) constant average cost per operation. Therefore, the runtime for storing $A$ and $B$ as hash tables is $O(a + b)$, and looping over (distinct) elements in $A$ and looking them up in the hash table of $B$ has runtime $a \cdot O(1) = O(a)$, which leads to an overall runtime of $O(a + b)$. This is as good as we can hope for in terms of asymptotic runtime complexity since any algorithm for computing $A \cap B$ would necessarily have to access all of the elements of both $A$ and $B$, which is an $O(a + b)$ operation.

In the collections module of the Python Standard Library there are container datatypes defaultdict and Counter which are subclasses of dict, Python’s built-in hash table implementation, with a few specialised methods which make coding up the algorithm described above simpler and faster than using the dict.setdefault() method.

from collections import defaultdict

def counts_dict(mylist: list) -> defaultdict:
    d = defaultdict(int) # Sets default count of each key to int() = 0
    for key in mylist:
        d[key] += 1
    return d

def intersection_with_hash_table(A: list, B: list) -> dict:
    result = dict()
    A = counts_dict(A)
    B = counts_dict(B)
    for key in set(A.keys()).intersection(B.keys()):
        result[key] = min(A[key], B[key])
    return result

The winning implementation in terms of combination of efficiency and simplicity is as follows:

from collections import Counter

def intersection_pythonic(A: list, B: list) -> Counter:
    return Counter(A) & Counter(B)

Tags: Multiset, multiplicity, Set theory, algorithms, hash table, sorting, data structures

References:

SQ10. Number patterns and properties

Sort the following $16$ numbers into $4$ sets of $4$ and give an explanation for each grouping: $\{ 1, 2, 3, 4, 4, 5, 5, 8, 9, 11, 13, 17, 25, 32, 49, 128 \}$.

SQ10 Solution

This question allows for multiple interpretations, especially for those familiar with the On-Line Encyclopedia of Integer Sequences (OEIS), but a possible grouping might be as follows:

Tags: Number theory, patterns

SQ11. Logarithms and continued fractions

Given $$ \log_{2}(11) = 3 + \cfrac{1}{2 + \cfrac{1}{5 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{25 + \cfrac{1}{1 + \cdots}}}}}}} $$ which is larger, $2^{128}$ or $11^{37}$?

SQ11 Solution

As $\log_{2}$ is an increasing function it suffices to compare the numbers $\log_{2}(2^{128}) = 128$ and $\log_{2}(11^{37}) = 37 \log_{2}(11)$.

For $x > 0$, it follows that $$\cfrac{1}{1 + x} < \cfrac{1}{1 + 0} = 1$$ $$\cfrac{1}{25 + \cfrac{1}{1 + x}} > \cfrac{1}{25 + \cfrac{1}{1 + 0}} = \frac{1}{26}$$ $$\cfrac{1}{1 + \cfrac{1}{25 + \cfrac{1}{1 + x}}} < \cfrac{1}{1 + \cfrac{1}{25 + \cfrac{1}{1 + 0}}} = \frac{26}{27}$$ $$\vdots$$ $$ \cfrac{1}{2 + \cfrac{1}{5 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{25 + \cfrac{1}{1 + x}}}}}}} < \cfrac{1}{2 + \cfrac{1}{5 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{25 + \cfrac{1}{1 + 0}}}}}}} = \frac{453}{986} $$ Therefore, $37 \log_{2}(11) < 111 + 37 \cdot \frac{453}{986}$. At this point we suspect that $111 + 37 \cdot \frac{453}{986} < 128$ which is equivalent to $37 \cdot \frac{453}{986} < 17$, which we can verify by calculating $$37 \cdot 453 = 16761 < 16762 = 17 \cdot 986.$$ Therefore, we have shown that $\log_{2}(11^{37}) < 111 + 37 \cdot \frac{453}{986} = 128 - \frac{1}{986} < 128$ and hence $11^{37} < 2^{128}$.

A similar line of reasoning with $x < 1$ allows us to bound $\frac{889}{1935} < \log_{2}(11) - 3 < \frac{453}{986}$.

Tags: Continued fractions, logarithms

References:

SQ12. Maximum power-of-2 factor of factorial numbers

Write $n! = 2^{a}b$ where $b, n \in \mathbb{N}$ and $a \in \mathbb{N} \cup \{ 0 \}$. Prove that $a < n$.

SQ12 Solution

For fixed $n \in \mathbb{N}$ there may be multiple ways to express $n! = 2^{a}b$ with $b \in \mathbb{N}$ and $a \in \mathbb{N} \cup \{ 0 \}$, and we are interested in when $a$ is as large as possible, so that we are extracting the largest possible power of $2$ from $n!$ as a factor.

Let $a_{n} := \max \{ a \in \mathbb{N} \cup \{ 0 \} : \exists b \in \mathbb{N} \text{ such that } n! = 2^{a}b \}$. It suffices to show that $a_{n} < n$ for all $n \in \mathbb{N}$.

The result holds for $n = 1$, in which case $1! = 1$ and $a_{1} = 0$, and for $n = 2$, in which case $2! = 2$ and $a_{2} = 1$. Notice that if $n$ is even, then $a_{n+1} = a_{n}$ since $(n + 1)! = (n + 1) \cdot n!$ where $n + 1$ is not divisible by $2$.

We define the $2$-adic valuation of a positive integer $m \in \mathbb{N}$ to be $$\nu_{2}(m) = \max \{ v \in \mathbb{N} \cup \{ 0 \} : 2^{v} \text{ divides } m \}.$$ Notice that by the unique prime factorisation of positive integers it follows that $\nu_{2}(m_{1} \cdot m_{2}) = \nu_{2}(m_{1}) + \nu_{2}(m_{2})$ and therefore by our definition above $$a_{n} = \nu_{2}(n!) = \sum_{i = 1}^{n} \nu_{2}(i).$$

We observed that odd numbers have $2$-adic valuation equal to zero, that is $\nu_{2}(2k + 1) = 0$ for all $k \ge 0$, whilst even numbers have $2$-adic valuation greater than $1$, that is $\nu_{2}(2k) \ge 1$ for all $k \in \mathbb{N}$. Moreover, singly even positive integers (of the form $4k + 2$) have $2$-adic valuation exactly $1$, $\nu_{2}(4k + 2) = 1$ for all $k \ge 0$, whilst doubly even positive integers (of the form $4k$) have $2$-adic valuation at least $2$, i.e. $\nu_{2}(4k) \ge 2$ for all $k \in \mathbb{N}$.

This generalises to the fact $\nu_{2}^{-1}(m) = \left( 2^{m + 1} \mathbb{Z} + 2^{m} \right) \cap \mathbb{N}$ for all $m \ge 0$.

Therefore, one way to express $a_{n} = \nu_{2}(n!)$ is $$a_{n} = \nu_{2}(n!) = \sum_{i = 1}^{n} \nu_{2}(i) = \sum_{k = 1}^{\lfloor \log_{2}{n} \rfloor} \Bigl \lfloor \frac{n}{2^k} \Bigr \rfloor < \sum_{k = 1}^{\infty} \frac{n}{2^k} = n.$$ The idea is to count one towards $a_{n}$ for each even number less than (or equal to) $n$, then count an additional one for each multiple of 4 less than (or equal to) $n$, and then count an extra one for each multiple of 8 less than (or equal to) $n$, and so on for all powers of $2$. Each time we add $1$ to the count represents another factor of $2$ in the factorial $n!$, and we can represent these counts using floor functions.

Tags: Number theory, p-adic valuation

References:

Longer Questions

LQ1. Rock, Paper, Scissors

Alice and Bob play Rock, Paper, Scissors until one or the other is 5 wins ahead. They generate their wins at random, so, in each round, the outcomes are equiprobably win, lose or draw. After 10 rounds, Alice is 1 ahead. After 13 rounds, one or the other is 1 ahead. At round 20, one of them attains the 5 win lead and the game ends. What is the probability that Alice is the ultimate winner?

LQ1 Solution

A principled way to approach this question would be to model the process as a Markov chain, similar to SQ6. Let $x_{t}$ be size of Alice’s lead in round $t$. Then, in general, we have state space $x_{t} \in \{ 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5 \}$ and transition probabilities $(p_{i,i-1}, p_{i,i}, p_{i,i+1}) = (1/3, 1/3, 1/3)$ for states $-4 \le i \le 4$, and absorbing states $-5$ and $5$. We are given the specific information that $x_{0} = 0$, $x_{10} = 1$, $x_{13} \in \{ -1, 1 \}$, $x_{20} \in \{ -5, 5 \}$, and $x_{t} \notin \{ -5, 5 \}$ for $t < 20$.

Due to the memoryless property, we need only consider the process from round 10 ($t = 10$) onwards, when Alice has a lead of $1$. We could then combine this model with conditional probability calculations based on the information provided in the question. Ultimately, we wish to calculate $$ P(x_{20} = -5 | x_{20} \in \{ -5, 5 \}, x_{13} \in \{ -1, 1 \}, x_{10} = -1, x_{t} \notin \{ -5, 5 \} \text{ for } t < 20) $$

We will follow this principled approach later to verify our answer, but first use a quicker method which does not require matrix multiplication.

Given that Alice has a lead of $1$ at round 10 and we know that at round 13 Alice has a lead of either $1$ or $-1$ (i.e. Bob leads by $1$), we can deduce that at round 13 Alice has a lead of $1$ with probability $\frac{7}{10}$ and a lead of $-1$ with probability $\frac{3}{10}$.

For Alice to make a net loss of $2$ over three rounds the sequence of outcomes would have to consist of a permutation of $2$ losses and $1$ draw $(D + 2L)$, for which there are $3$ possibilities; whilst making a net gain/loss of $0$ over three rounds requires a permutation of either one win, one loss, and one draw $(D + L + W)$, or three draws $(3D)$, for which there are $6 + 1 = 7$ possibilities. Then, as each set of outcomes subject to the constraints is equally likely, we obtain the probabilities $\frac{3}{3 + 7}$ and $\frac{7}{3 + 7}$.

Next, we consider the number of sequences of outcomes over seven rounds that could lead the player who has a lead of $1$ at round 13 to have a lead of either $5$ or $-5$ at round 20 causing the game to end.

For the net loss of $6$ over 7 rounds, the outcomes must be $6$ losses and $1$ draw $(D + 6L)$, where the last loss must come at the end of the sequence in round 20 so that the game doesn’t end earlier, which gives $6$ possibilities according to which round the draw happens.

For a net gain of $4$ over 7 rounds, the set of outcomes can be either $(3D + 4W)$ or $(D + L + 5W)$, where we must take care not to count cases where the game ends before round 20. For the case of $4$ wins and $3$ draws, it suffices to require the last win to occur in round 20, after which we count the possible permutations of the set $(3D + 3W)$ of which there are $6!/(3!)^{2} = 20$.

For the player with a lead of $1$ in round 13 to ultimately win the game in round 20 by making $5$ wins, $1$ loss, and $1$ draw, the last win must occur in round 20 to avoid the game ending early. From the remaining $30 = 6 \times 5$ configurations of $(D + L + 4W)$ we exclude the $5$ in which the loss occurs in round 19 (since that would imply a lead of $5$ before round 20), and the specific sequence of outcomes $(WWWWLD)$, for which the game would actually have ended in round 18, leaving $24 = 30 - 5 - 1$ valid sequences.

Therefore, if a player is leading by $1$ in round 13 and we know that the game ends in round 20, there is a probability of $\frac{44}{50} = \frac{22}{25}$ that this player wins and a probability of $\frac{6}{50} = \frac{3}{25}$ that they lose.

Combining all of this information together, we find that the probability that Alice is the ultimate winner is $$\frac{7}{10} \cdot \frac{22}{25} + \frac{3}{10} \cdot \frac{3}{25} = \frac{163}{250} = 65.2\%$$ by aggregating the possibility that she retains the lead of $1$ at round 13 and goes on to win overall in round 20 with the possibility that she pulls back from trailing by $1$ in round 13 to claim victory in round 20.

The Python code listing below models the problem as an Absorbing Markov Chain and calculates the probability that Alice wins the game by analysing powers of the transition matrix multiplied by vector probability distribution of the state at times $t = 1-$, when $P(x_{10} = 1) = 1$, and $t = 13$, when $P(x_{13} \in \{ -1, 1 \}) = 1$.

This code can be run to verify the above derivation of Alice’s winning probability by clicking the Evaluate button beneath the code listing.

import numpy as np
from fractions import Fraction

# Set up the transition matrix
P = np.zeros((11, 11), dtype='object')

for i in range(1, 10):
    P[i, i-1:i+2] = Fraction(1, 3)

# Absorbing states (-5, 5 coded as index 0, 10, respectively)
P[0, 0] = Fraction(1)
P[10, 10] = Fraction(1)

# Alice leads by 1 in round 10 (coded as index 6 = 5 + 1)
x10 = np.zeros(11, dtype='object')
x10[6] = Fraction(1)

# Probability distribution of (transient) states in round 13
x13 = np.linalg.matrix_power(P, 3).dot(x10)

# Condition on being in state -1 or 1 at round 13 (index 4 and 6, resp.)
x13_normalised = np.zeros(11, dtype='object')
x13_normalised[4] = x13[4] / (x13[4] + x13[6])
x13_normalised[6] = x13[6] / (x13[4] + x13[6])

# Probability distribution of transient states in round 19
x19 = np.linalg.matrix_power(P, 6).dot(x13_normalised)

# Condition on being in state -5 or 5 at round 20
results = {"Alice win": x19[9] / (x19[1] + x19[9]),
           "Alice lose": x19[1] / (x19[1] + x19[9])}
print(results) # {'Alice win': Fraction(163, 250), 'Alice lose': Fraction(87, 250)}
print(float(results["Alice win"])) # 0.652

Tags: Probability, Markov Chains

Related Reading:

LQ2. The signal and the noise

You are monitoring a data stream which is delivering very many $32$-bit quantities at a rate of $10$ Megabytes per second. You know that either:

  1. All values occur equally often, or
  2. Half of the values occur $2^{10}$ times more often than others (but you dont know anything about which would be the more common values).

You are allowed to read the values off the data stream, but you only have $2^{20}$ bytes of memory. Describe a method for determining which of the two situations, 1 or 2, occurs. Roughly how many data values do you need to read to be confident of your result with a probability of $0.999$? (This is about the $3$ sigma level – $3$ standard deviations of a normal distribution.)

LQ2 Initial Ideas and Solution

An example of a 32-bit quantity could be a single 4-byte unsigned long int representing an integer ranging from $0$ to $2^{32} - 1$. In $2^{20} = 1,048,576$ bytes of memory (i.e. 1MB, which is approximately $1$ million bytes), we could hold $2^{18} = 262144$ many 4-byte (a.k.a. 32-bit) quantities.

In scenario 1, each 32-bit quantity would occur equally often with probability $\frac{1}{2^{32}}$ (a discrete uniform distribution). Whereas in scenario 2, the uncommon values would occur with probability $x$ and the common values would occur with probability $2^{10} x$. As we know half of the values (i.e. $2^{31}$ out of $2^{32}$) are uncommon and the other half are common, we can deduce that $x = \frac{1}{2^{31}(1 + 2^{10})}$.

Idea 1. Compare mean and variance

Given suitable time and modest luck, we would be able to distinguish scenario 2 simply by looking at the running mean and variance/standard deviation of the received data values and comparing them with the mean $\mu = 2^{31} - \frac{1}{2}$ and variance $\sigma^{2} = \frac{1}{12} (2^{64} - 1)$ of a discrete uniform distribution over $2^{32}$ values from scenario 1 (as the null hypothesis). This is because, assuming that the common and uncommon values of scenario 2 are chosen at random it is probable that this will introduce noticeable skew into the subsequent distribution, in which case the problem becomes a matter of computation/runtime, whilst memory requirements for this method are modest (we don’t have to store values for long).

However, the question states that we cannot assume anything about the distribution of more common values in scenario 2, in which case the above method could be compromised if we chose, say, for the even numbers in the range to be more common and the odd numbers to be uncommon (or vice versa), since this might lead to similar mean and variance as the uniformly distributed case. For more details on how to keep track of the running mean and variance of values from a data stream whilst keeping memory requirements low, see this Wikipedia article.

Idea 2. Hypothesis testing on observed distributions

Given greater memory capacity than provided in the question, we might compare the empirical distribution of observed data values to an idealised uniform distribution (scenario 1) by applying more sophisticated methods such as the Kolmogorov–Smirnov test or a Chi-squared test. The former is a quantitative analogue of eyeballing the graphs of the cumulative distribution functions of the sample distribution and the null hypothesis distribution, whilst the latter is the analogue of comparing the (normalised) histogram of a sample with the probability density function of the null hypothesis distribution.

The Kolmogorov–Smirnov test is a quantitative method for comparing the cumulative distribution functions of two distributions by measuring the largest vertical distance between the two graphs. The CDF of a uniform distribution increases in a linear fashion as $F(k) = \frac{k+1}{2^{32}}$ for $k = 0, 1, \ldots, 2^{32} - 1$, whilst we would expect the empirical CDF in scenario 2 to be much more irregular in its steps. Subject to some simplifying assumptions, to reject the null hypothesis (scenario 1) at the $0.999$ confidence level we would need to see $$\sqrt{n} D_{n} = \sqrt{n} \max_{k}|F_{n}(k) - F(k)| > \sqrt{\frac{1}{2} \log_{e} (\frac{2}{1 - 0.999})} \approx 1.9495$$ where $F_{n}(k)$ is the empirical distribution function for a sample of size $n$.

We can calculate the Chi-squared test statistic $$\chi^{2} = \sum_{k=0}^{2^{32} - 1} \frac{(O_{k} - E_{k})^{2}}{E_{k}}$$ where $E_{k} = \frac{n}{2^{32}}$ is the expected theoretical frequency of value $k$ from $n$ samples of the uniform distribution of scenario 1, and $O_{k}$ is the number of observations of value $k$ (which would mostly be zero for small $n < 2^{31}$). Under the null hypothesis, this test statistic would have a chi-square distribution with $2^{32} - 1$ degrees of freedom, or we could divide by this number to obtain a standard normal $z$-test statistic under the null hypothesis. As we frequently divide by small numbers in this calculation, there is a risk of loss of precision and/or numerical underflow, so the likelihood-ratio significance test statistic (a.k.a. G-test) which uses logarithms may be more appropriate: $$G = 2 \sum_{k} O_{k} \cdot \log_{e} (\frac{O_{k}}{E_{k}})$$

A key challenge and limitation to the above approaches using frequency tests for uniformity is that, in principle, we should keep track of the counts of all $2^{32}$ possible values to perform the calculations, which would require half a gigabyte of memory ($2^{29}$ bytes) to store a bit vector mapping of every possible value, but we only have $2^{20}$ bytes of memory at our disposal. Two possible workarounds include:

  1. Bigger histogram bins - group the $2^{32}$ values into modestly sized bins, which would remain uniformly distributed in scenario 1, when reading/counting the frequency of occurences before performing hypothesis testing. This will effect the expected and actual number items in each bin.
  2. Reach a decision on whether we are in scenario 1 or 2 based on the limited amount of data we can record in a dictionary/hash table of values and counts given the memory we have. We can still calculate the KS and Chi-squared test statistics with small sample sizes $n < 2^{18}$ using the knowledge that any values not stored in our counting dictionary have zero frequency. The question in this case is whether the tests will be powerful enough to reject the null hypothesis when we are in scenario 2 (requiring a reasonable number of repeated values before we fill memory capacity).
Idea 3. Hypothesis testing on repeat times

These above methods may be somewhat memory intensive given the number of possible data values, so an alternative would be to store a bunch of values off the data stream and then measure the times until those values are seen again and/or count the number of repetitions in a given time. This alternative method might involve reading relatively more data values from the stream/taking a longer time to reach a conclusion depending on implementation details.

Suppose that we stored $n$ many $32$-bit quantities in memory as keys, using $4n$ bytes and leaving $2^{20} - 4n$ bytes of memory leftover to store data on the timing/number of observations of the stored values.

In scenario 1, each value has probability $\frac{1}{2^{32}}$ of occuring in any given observation, and the expected frequency a given value occurs is once in every $2^{32}$ observations. With a data rate of $10$ Megabytes per second and $4$ bytes per observed value, this means we would expect to see any given value repeated once every $\frac{2^{32}}{10 \cdot 2^{18}} = 1638.4$ seconds, or equivalently $27$ minutes and $18.4$ seconds.

In scenario 2, the common values have probability $\frac{2^{10}}{2^{31}(1 + 2^{10})} \approx \frac{1}{2^{31}}$ of occuring, whilst the uncommon values have probability $\frac{1}{2^{31}(1 + 2^{10})} \approx \frac{1}{2^{41}}$ of occuring in any given observation. Therefore, given a specific commonly occuring data value, we would expect to see it once in every $\frac{2^{31}(1 + 2^{10})}{2^{10}}$ observations, or roughly twice as frequently given the same data rate - specifically, once every $820$ seconds ($13$ minutes and $40$ seconds). On the other hand, for a given less common data value, we would expect to see it once in every $2^{31}(1 + 2^{10})$ observations on average, which translates to an average repeat time $2^{10}$ times larger at $839680$ seconds, or equivalently around $9.72$ days.

In our initial sample of $n$ many $32$-bit quantities, we would expect the common values to occur $2^{10} = 1024$ times more frequently than the uncommon values, in accordance with the ratio of their probabilities. Specifically, on average we would expect our sample to consist of $\frac{n}{1025}$ uncommon values and $\frac{1024n}{1025}$ common values. The theoretical expected mean repeat time is actually the same for both scenarios 1 and 2, since $\frac{1024}{1025} \cdot 820 + \frac{1}{1025} \cdot 839680 = 1638.4$ seconds, however we would be able to distinguish these two cases by either stopping measurement after about $15$ or $30$ minutes (or equivalently after reading about 9-18GB of data) to avoid the extreme outlier waiting times, or otherwise using a different way to measure the distribution of repeat times (mode, median, quartiles/box plot, histogram).

Further analysis into the variance of expected times between occurences of a given value in each scenario is needed to definitively state how much data would be required to distinguish between scenario 1 and 2 with confidence probability $0.999$ (mean repeat time $820$ seconds vs. $1640$ seconds). Upon further consideration and reflection, it appears that modelling the number of repetitions observed of values from the stored collection over a fixed time using a Poisson distribution would be an ideal way to model the problem. The assumption that the number of occurences of a given value is distributed as a Poisson random variable holds, and by independence we may take the sum of occurences within a given set to also be Poisson distributed.

Suppose we used the full $2^{20} = 1,048,576$ bytes of memory to store $2^{18} = 262144$ many 4-byte (a.k.a. 32-bit) quantities, and had a few bytes of memory left over to keep count of how many subsequent data values read fell into our stored set and do some statistical calculations. Then the probability/average event rate of a newly read value being one of the values stored in memory (a.k.a. the rate parameter $\lambda$ for a single observation) would be $\lambda_{1} = \frac{2^{18}}{2^{32}} = \frac{1}{2^{14}}$ in scenario 1, and $$\lambda_{2} = \frac{2^{18}}{2^{31}} \left( \left( \frac{1024}{1025} \right)^{2} + \left( \frac{1}{1025} \right)^{2} \right) \approx 0.998 \cdot \frac{1}{2^{13}}$$ in scenario 2.

If we read $n$ values from the data stream and count the number $X_{n}$ of these which lie in our stored set of $2^{18}$ values, we can model this as a Poisson distributed random variable with rate parameter (also mean and variance) $\lambda_{1} n = \frac{n}{2^{14}}$ in scenario 1, or otherwise $\lambda_{2} n \approx \frac{n}{2^{13}}$ in scenario 2. We would like to know for which $n$ are we able to distinguish between $\mathrm{Pois}(\frac{n}{2^{14}})$ and $\mathrm{Pois}(\frac{n}{2^{13}})$ with confidence probability $0.999$. This will occur for sufficiently large $n$ such that there exists an integer $k \ge 0$ for which $$P(X_{n} \le k | X_{n} \sim \mathrm{Pois}(\frac{n}{2^{14}})) \ge 0.999 \text{ and } P(X_{n} > k | X_{n} \sim \mathrm{Pois}(\frac{n}{2^{13}})) \ge 0.999$$

In other words, when there is very little probability of overlap between the two distributions we can distinguish between the two by a sampled value.

For Poisson distributions with sufficiently large rate parameter, say $\lambda > 1000$ (or $\lambda > 10$ with continuity correction), we may reasonably approximate $\mathrm{Pois}(\lambda)$ by the normal distribution $\mathrm{Norm}(\mu = \lambda, \sigma^{2} = \lambda)$ and exploit the fact that $99.73%$ of the probability density of a normal distribution lies within three standard deviations of the mean. Therefore, we wish to find $n$ large enough that $$\frac{n}{2^{14}} + 3 \sqrt{\frac{n}{2^{14}}} \le \frac{n}{2^{13}} - 3 \sqrt{\frac{n}{2^{13}}}$$

We may rearrange this inequality as $\sqrt{n} \ge 2^{7} \cdot 3 \cdot (1 + \sqrt{2}) \approx 927$ to find $n \ge 2^{2 \log_{2}(927)} \approx 2^{19.71} \approx 860000$. Therefore, we can far improve on our previous methods and distinguish between the two scenarios in under $1$ second (assuming fast memory writing and lookup speeds, such as by using statically allocated memory and hashed values) as follows:

  1. Use $2^{20}$ bytes of memory to store $2^{18}$ many 32-bit quantities as a set $S$. This takes $0.1$ seconds of reading time.
  2. Read an additional $2^{20}$ data values from the stream, taking $0.4$ seconds, and count the number $X$ of these values which lie in $S$.
  3. Either all values occur equally often, in which case $X \sim \mathrm{Pois}(\frac{2^{20} \cdot 2^{18}}{2^{32}}) = \mathrm{Pois}(2^{6})$, or half of the values occur $2^{10}$ times more often than others, in which case $X \sim \mathrm{Pois}(2^{7})$.
  4. Approximate $\mathrm{Pois}(2^{6}) \approx \mathrm{Norm}(64, 8)$ and $\mathrm{Pois}(2^{7}) \approx \mathrm{Norm}(128, 8 \sqrt{2})$ so that if $X \le 64 + 3 \cdot 8 = 88$ we are in scenario 1 (32-bit quantities are uniformly distributed), whereas if $X > 88 < 128 - 3 \cdot 8 \sqrt{2}$ we know that half of the values occur $2^{10}$ times more often than others (i.e. scenario 2), with probability at least $0.999$.

Tags: Statistics, Hypothesis testing, uniform distribution, Poisson distribution

References:

LQ3. Asymptotic number of tilings

A $2 \times N$ rectangle is to be tiled with $1 \times 1$ and $2 \times 1$ tiles. Prove that the number of possible tilings tends to $kx^{N}$ as $N$ gets large. Find $x$, to $2$ decimal places.

LQ3 Solution

LQ3 Initial Ideas

Does the problem description mean to imply that the $2 \times 1$ tiles must always be placed vertically? Probably not. If this was the case, the number of tilings of a $2 \times N$ rectangle would be exactly $2^{N}$ since we could decompose it into $N$ many $2 \times 1$ rectangles, each of which independently permits $2$ possible tilings. We will assume any $2 \times 1$ tiles can be placed either horizontally or vertically inside the rectangle, in which case $2^{N}$ now serves as a lower bound to the number of possible tilings.

Once we have proven that the number of possible tilings tends to $kx^{N}$ as $N$ gets large, we could approximate $x$ using the ratio of empirical values. Let $a_{N}$ denote the number of possible tilings of a $2 \times N$ rectangle by $1 \times 1$ and $2 \times 1$ tiles. Then as $N$ gets large we have $\frac{a_{N+1}}{a_{N}} \approx \frac{kx^{N+1}}{kx^{N}} = x$.

It is likely that $a_{N}$ satisfies a recurrence relation, but care will need to be taken to avoid double-counting.

Finding the recurrence relation: Method 1

For $N \ge 3$ there are exactly two tilings of a $2 \times N$ rectangle which cannot be decomposed into separate tilings of a $2 \times k$ rectangle and a $2 \times (N - k)$ rectangle for some $1 \le k \le N-1$. The number of ‘irreducible’ tilings of a $2 \times 1$ rectangle is also $2$, whilst the number of irreducible tilings of a $2 \times 2$ rectangle is $3$.

Many of the tilings of a $2 \times N$ rectangle which are reducible/decomposable could be considered as the concatenation of a $2 \times (N - 1)$ tiling with a $2 \times 1$ tiling, either on the left or on the right. The overlap of these two types of decomposition (which we must avoid double counting) are those which can be decomposed as a $2 \times (N - 2)$ tiling combined with separate $2 \times 1$ tilings on both left and right.

However, this doesn’t actually count all decompositions because, for example, we could have a $2 \times 4$ rectangle decomposed into two irreducible $2 \times 2$ tilings. We deduce that $a_{1} = 2$, $a_{2} = 7$, $a_{3} = 22$, and for $N \ge 3$ we have the following lower bound: $$a_{N} \ge 2 + a_{1} a_{N-1} + a_{N-1} a_{1} - a_{1} a_{N-2} a_{1} = 2 + 4(a_{N-1} - a_{N-2})$$

Instead, when we know that a $2 \times N$ tiling is reducible, we can split it into a $2 \times k$ irreducible tiling and a $2 \times (N - k)$ arbitrary tiling for some $1 \le k \le N-1$. By also taking into account the irreducible $2 \times N$ tilings, we obtain the following reccurence relation for $N \ge 2$: $$a_{N} = a_{N-2} + 2 \sum_{k=0}^{N-1} a_{k}$$ where $a_{0} = 1$. The additional $a_{N-2}$ term comes from the fact that there are $3$ irreducible $2 \times 2$ tilings rather than only $2$.

By considering the next term in the sequence we are able to obtain a homogeneous linear recurrence relation of order 3 with constant coefficients: $$a_{N+1} = 3 a_{N} + a_{N-1} - a_{N-2}$$

Finding the recurrence relation: Method 2

There is an alternative way to derive the same recurrence relations on the number $a_{N}$ of possible tilings of a $2 \times N$ rectangle by $1 \times 1$ and $2 \times 1$ tiles. Consider a $2 \times N$ rectangle with a $1 \times 1$ corner tile removed, and let $b_{N}$ denote the number of tilings of this shape by $1 \times 1$ and $2 \times 1$ tiles. Then $a_{1} = 2$ and $b_{1} = 1$. By partitioning tilings contributing to $a_{N}$ according to the type and orientation of the tile passing through the top left corner square, when $N \ge 2$ we split the tilings into three subsets:

  1. If the tile passing through the top left corner square is a $1 \times 1$ tile, the corresponding subset of tilings is counted by $b_{N}$.
  2. If the tile passing through the top left corner square is a domino placed vertically, the corresponding subset of tilings is counted by $a_{N-1}$.
  3. If the tile at the top left corner is a horizontal domino, we further break down this subset according to the tile on the bottom left square:
    1. If additionally the bottom left square contains a $1 \times 1$ tile, the corresponding subset of tilings is counted by $b_{N-1}$.
    2. Otherwise, if the bottom left square is covered by another horizontal domino, then the corresponding subset of tilings is counted by $a_{N-2}$.

Therefore, for $N \ge 2$ we may write $$a_{N} = b_{N} + a_{N-1} + b_{N-1} + a_{N-2}$$

We may apply a similar analysis on tilings counted by $b_{N}$, partitioning according the tile over the corner square outside the $2 \times (N - 1)$ rectangle, to find that $b_{N} = a_{N - 1} + b_{N - 1}$ for $N \ge 2$. We may apply a telescoping sum to the relation $b_{N} - b_{N - 1} = a_{N - 1}$ to find that $$a_{N-1} + a_{N-2} + \ldots + a_{1} = \sum_{k=2}^{N} a_{k-1} = \sum_{k=2}^{N} (b_{k} - b_{k-1}) = b_{N} - b_{1} = b_{N} - 1$$

By letting $a_{0} = 1$, we find that $b_{N} = \sum_{k=0}^{N-1} a_{k} = a_{N - 1} + b_{N - 1}$, then we may substitute to find that $$a_{N} = b_{N} + a_{N-1} + b_{N-1} + a_{N-2} = a_{N-2} + 2 \sum_{k=0}^{N-1} a_{k}$$ Then, once again, $a_{N+1} - a_{N} = 2 a_{N} + a_{N-1} - a_{N-2}$. Thus we obtain the homogeneous linear recurrence relation of order 3 with constant coefficients: $$a_{N+1} - 3 a_{N} - a_{N-1} + a_{N-2} = 0$$

Determining asymptotic behaviour

The form of solutions to a homogeneous linear recurrence relation are well known. If $x_{1}, x_{2}, x_{3}$ are solutions/roots to the auxiliary equation $x^{3} - 3x^{2} - x + 1 = 0$, then we may express $a_{N} = k_{1} x_{1}^{N} + k_{2} x_{2}^{N} + k_{3} x_{3}^{N}$, where the coefficients $k_{1}, k_{2}, k_{3}$ are such that the initial conditions $a_{0} = 1, a_{1} = 2, a_{2} = 7$ are satisfied.

We now proceed to analyse the auxiliary equation $p(x) = x^{3} - 3x^{2} - x + 1 = 0$ and its roots. Consider that $p(-1) = -2$, $p(0) = 1$, $p(1) = -2$, $p(2) = -5$, $p(3) = -2$, $p(4) = 13$. By using the intermediate value theorem, or knowledge of the shape of a cubic polynomial, we can conclude that the three roots of $p$ can be ordered $-1 < x_{3} < 0 < x_{2} < 1 < 3 < x_{1} < 4$. In particular, since $0 < |x_{2}|, |x_{3}| < 1$ we have $\lim_{N \to \infty} (k_{2} x_{2}^{N} + k_{3} x_{3}^{N}) = 0$, so $a_{N} \to k_{1} x_{1}^{N}$ as $N$ gets large, as required.

It remains to approximate the root $3 < x_{1} < 4$ to the cubic polynomial $p(x) = x^{3} - 3x^{2} - x + 1$. One way to do this is to proceed with the divide and conquer strategy of repeatedly evaluating $p(x)$ and using the intermediate value theorem to obtain successively tighter bounds on $x_{1}$.

$x$ $\mathrm{sign}(p(x))$ Lower bound Upper bound
$3$ Negative $3$
$4$ Positive $3$ $4$
$3.5$ Positive $3$ $3.5$
$3.25$ Positive $3$ $3.25$
$3.125$ Negative $3.125$ $3.25$
$3.1875$ Negative $3.1875$ $3.25$
$\frac{103}{32} = 3.21875$ Positive $3.1875$ $3.21875$
$\frac{205}{64}$ Negative $3.203125$ $3.21875$
$\frac{411}{128}$ Negative $3.2109375$ $3.21875$
$\frac{823}{256}$ Positive $3.2109375 = \frac{411}{128}$ $3.21484375 = \frac{823}{256}$

Therefore, the number of possible tilings of a $2 \times N$ rectangle by $1 \times 1$ and $2 \times 1$ tiles tends to $kx^{N}$ as $N$ gets large, where $x$ is the largest root of the cubic polynomial $p(x) = x^{3} - 3x^{2} - x + 1$. We have deduced that $\frac{411}{128} = 3.2109375 < x < 3.21484375 = \frac{823}{256}$, and so $x \approx 3.21$ to $2$ decimal places.

A quicker way to approximate the desired root of $p(x) = 0$ would be to use the Newton–Raphson method which converges at least quadratically for a root of multiplicity $1$ (i.e. not a repeated root) in a neighbourhood of the root, which intuitively means that the number of correct digits roughly doubles in every step. The Newton-Raphson iteration step is $$ x_{n+1} = x_{n} - \frac{p(x_{n})}{p’(x_{n})} = x_{n} - \frac{x_{n}^{3} - 3x_{n}^{2} - x_{n} + 1}{3x_{n}^{2} - 6x_{n} - 1} = \frac{2x_{n}^{3} - 3x_{n}^{2} - 1}{3x_{n}^{2} - 6x_{n} - 1} $$ and we will use an initial approximation $x_{0} = 3$. Then $x_{1} = \frac{13}{4} = 3.25$, $x_{2} = \frac{1151}{358} = 3.2150838…$, and $x_{3} = 3.21432…$, with $x_{4} = 3.214319743…$ stabilising up to the precision on a typical handheld calculator. Therefore, $x \approx 3.21$ to $2$ decimal places, and $x \approx 3.214319743$ to $9$ decimal places.

With a little further calculation, we can show that the solution to $a_{N+1} = 3 a_{N} + a_{N-1} - a_{N-2}$ where $a_{0} = 1, a_{1} = 2, a_{2} = 7$ is $a_{N} = k_{1} x_{1}^{N} + k_{2} x_{2}^{N} + k_{3} x_{3}^{N}$ where, up to around 10 significant figures, we have:

$i$ $x_{i}$ $x_{i}^{2}$ $k_{i}$
$1$ $3.214319743$ $10.33185141$ $0.6645913847$
$2$ $0.4608111272$ $0.212346895$ $0.07943671576$
$3$ $-0.6751308706$ $0.4558016924$ $0.2559718995$

When it comes to calculating actual values of $a_{N}$, the recurrence formula is faster and more accurate, requiring fewer and simpler operations whilst ensuring no loss of precision/integer output at each iteration. The asymptotic behaviour $a_{N} \approx O(3.21^{N})$ is useful to know if we are iterating over tilings of a $2 \times N$ rectangle by $1 \times 1$ and $2 \times 1$ tiles as part of a larger algorithm.

Tags: Recurrence relation, Numerical analysis

References:

Tags: Dynamic programming

LQ4. Prime Power Divisors

The Prime Power Divisors (PPD) of a positive integer are the largest prime powers that divide it. For example, the PPD of $450$ are $2$, $9$, $25$. Which numbers are equal to the sum of their PPD?

LQ4 Solution

Powers of prime numbers are trivially equal to the sum of their prime power divisors, and these are the only numbers with this property. Let $f : \mathbb{N} \to \mathbb{N}$ be the function which maps a positive integer to the sum of its prime power divisors. So $f(1) = 0$, $f(6) = 2 + 3 = 5$, $f(450) = 2 + 9 + 25 = 36$, and $f(p^{k}) = p^{k}$ for $p$ prime and $k \in \mathbb{N}$. Note also that if $a, b$ are coprime, then $f(ab) = f(a) + f(b)$.

We claim that $f(n) \le n$ for all positive integers $n$, with equality if and only if $n$ is a prime power. Suppose, for contradiction, that the set of positive integers which are not a prime power but have $f(n) \ge n$ is nonempty, and let $n_{0}$ be the smallest element in this set. By assumption, we can express $n_{0}$ as a product of coprime integers $a, b \ge 2$ since $n_{0}$ is a composite number with at least two distinct prime factors. The factors $a$ and $b$ are distinct since they are coprime and both greater than $1$. Then $n_{0} \le f(n_{0}) = f(ab) = f(a) + f(b) \le a + b < 2 \max(a, b) \le ab = n_{0}$, which is a contradiction. Therefore, if $n$ is not a prime power, then $f(n) < n$. This completes the proof.

Tags: Number theory, prime factors

Related Reading:

LQ5. Parameters of a PRNG

$353, 46, 618, 30, 877, 235, 98, 24, 107, 188, 673$ are successive large powers of an integer $x$ modulo a 3-digit prime $p$. Find $x$ and $p$.

LQ5 Solution

This problem is related to cracking a pseudo-random number generator known as the Lehmer random number generator, which is a special case of a linear congruential generator. Determining $x$ and $p$ would allow us to calculate subsequent terms in the sequence. A subsequent problem could be find out which large powers of $x$ modulo $p$ these are, which is known as the discrete logarithm problem. As we are told these are successive powers of $x$ modulo $p$, one would only need to solve this problem for one number in the sequence.

We first determine $x$ by making use of Bézout’s identity and the Extended Euclidean algorithm. Label the elements of the sequence by $a_{n}$ for $n = 0, 1, \ldots, 10$. Then we have that $a_{n} x \equiv a_{n+1} \ (\mathrm{mod}\ p)$ for $n = 0, 1, \ldots, 9$. We would like to find indices $n_{1}, n_{2}$ such that $\gcd(a_{n_{1}}, a_{n_{2}}) = 1$, then apply Bézout’s identity/EEA to find integers $s, t$ such that $a_{n_{1}} s + a_{n_{2}} t = 1$. From this we could deduce $$x = (a_{n_{1}} s + a_{n_{2}} t) x = (a_{n_{1}} x) s + (a_{n_{2}} x) t \equiv a_{n_{1} + 1} s + a_{n_{2} + 1} t \ (\mathrm{mod}\ p)$$

We may assume that $p$ is a 3-digit prime number greater than the largest number appearing in the sequence, so $877 < p < 999$. If we are lucky, we will be able to find $n_{1}, n_{2}, s, t$ such that $0 < a_{n_{1} + 1} s + a_{n_{2} + 1} t < 881$ so that we have a primitive expression for $x \ (\mathrm{mod}\ p)$. Once we know $x$, we can determine $p$ by checking which 3-digit prime in the given range satisfies the equations $a_{n} x \equiv a_{n+1} \ (\mathrm{mod}\ p)$ for $n = 0, 1, \ldots, 9$. That is to say, we may check for 3-digit prime factors of $a_{n} x - a_{n+1}$.

We pick $a_{6} = 98$ and $a_{8} = 107$ (since we know $107$ is prime), so that $9 = 107 - 98$, $8 = 98 - 10 \cdot 9$, and $$1 = 9 - 8 = 9 - (98 - 10 \cdot 9) = 11 (107 - 98) - 98 = 11 \cdot 107 - 12 \cdot 98.$$ Thus $x = 11 \cdot 107 x - 12 \cdot 98 x \equiv 11 \cdot 188 - 12 \cdot 24 = 2068 - 288 = 1780 \ (\mathrm{mod}\ p)$. This is outside of the desired range, but will be useful once we find another expression for $x \ (\mathrm{mod}\ p)$ since we can determine $p$ by factoring the difference between the two expressions. We could then reduce $x$ modulo $p$ if necessary.

Next, we pick $a_{7} = 24$ and $a_{8} = 107$, so that $11 = 107 - 4 \cdot 24$, then $2 = 24 - 2 \cdot 11$, and $$1 = 11 - 5 \cdot 2 = 11 - 5 (24 - 2 \cdot 11) = 11 (107 - 4 \cdot 24) - 5 \cdot 24 = 11 \cdot 107 - 49 \cdot 24.$$ Therefore, $x = 11 \cdot 107 x - 49 \cdot 24 x \equiv 11 \cdot 188 - 49 \cdot 107 = 2068 - 5243 = -3175 \ (\mathrm{mod}\ p)$.

It follows that $1780 - (-3175) = 4955$ is a multiple of $p$, where $4955 = 5 \cdot 991$, so our 3-digit prime is $p = 991$. Consequently, we may write $x \equiv 1780 \equiv 789 \equiv -202 \ (\mathrm{mod}\ 991)$.

The following simple script calculates the discrete logarithm $\log_{789}(353)$ in $\mathbb{Z} / 991 \mathbb{Z}$. In particular we find that 353 = 789^62 mod 991. This brute-force ‘trial multiplication’ algorithm will not scale well as the prime $p$ increases.

x, p = 789, 991
target = 353
el = 1
x_pow = 0
while(el != target):
    x_pow += 1
    el *= x
    el %= p
print(f"{target} = {x}^{x_pow} mod {p}")

References:

LQ6. Complexity of triangulating a polygon

$(X_{1}, Y_{1}),(X_{2}, Y_{2}), \ldots, (X_{n}, Y_{n})$ are $n$ ordered points in the Cartesian plane that are successive vertices of a non-intersecting closed polygon. Describe how to find efficiently a diagonal (that is, a line joining 2 vertices) that lies entirely in the interior of the polygon. Repeated application of this process will completely triangulate the interior of the polygon. Estimate the worst case number of arithmetic operations needed to complete the triangulation.

LQ6 Initial Ideas and Discussion

A non-intersecting closed polygon with $n$ vertices can be triangulated by $n-3$ diagonals. By proceeding through the set of vertices cyclically (i.e. by taking indices modulo $n$), we check whether we can construct a valid diagonal from $P_{k}$ to $P_{k+2}$, starting from $k = 1$. If we cannot, we increment $k$ by $1$ and try again (see if there is a valid diagonal from $P_{k+1}$ to $P_{k+3}$). However, if we can draw a diagonal from $P_{k}$ to $P_{k+2}$ that lies entirely in the interior of the polygon, we add $(P_{k}, P_{k+2})$ to a list of vertex pairs describing diagonals in our triangulation, and remove $P_{k+1}$ from the list of vertices we consider for new diagonals and from the list of vertices we check when determining whether a diagonal is valid (i.e. repeat the process of triangulation on the the list of $n-1$ ordered points with $P_{k+1}$ removed), restarting the process at vertex $k+2$.

It remains to describe a method to verify whether the line segment between vertices $P_{k}$ and $P_{k+2}$ lies within the interior of a polygon. Initial thoughts include checking whether the line separates $P_{k+1}$ from the remaining vertices, by checking a line or dot product inequality, but this may be a sufficient but not necessary condition; or reasoning based on the angles between triplets of points $(P_{k}, P_{k+1}, P_{k+2})$.

It turns out this is the beginning of an implementation of a polygon triangulation algorithm known as the ear clipping method. This can run in

References:

LQ7. Semigroups

A semigroup is a set $S$ with an associative operation, which we will write as multiplication. That is, $x(yz) = (xy)z$ for all $x, y, z \in S$.

  1. Suppose that a finite semigroup $S$ has the property that for all $x \in S$ there is an integer $n > 1$ such that $x^{n} = x$. Is it true that S is, in fact, a group?
  2. Suppose that a finite semigroup $S$ has the property that for all $x \in S$ there is an integer $n$ such that $x^{n+1} = x^{n}$. Show that the only subsets of $S$ which form a group are of size $1$.

LQ7 Solution

The set $S = \{ 0, 1 \}$ forms an abelian semigroup with the usual multiplication of natural numbers, i.e. $0 \cdot 0 = 0$, $1 \cdot 1 = 1$, and $1 \cdot 1 = 0 \cdot 1 = 0$. Associativity is inherited as a sub-semigroup of the natural numbers $\mathbb{N}$, otherwise one could check the 8 possible products of three elements. This is an example of a finite semigroup satisfying property 1 above, as we have $x^{2} = x$ for all $x \in S$. Moreover, the element $1 \in S$ is the multiplicative identity. However, $S$ is not a group since $0 \in S$ has no inverse element in $S$. Therefore, a finite semigroup satisfying property 1 above is not necessarily a group.

Now suppose $S$ is a finite semigroup with the property that for all $x \in S$ there is an integer $n$ such that $x^{n+1} = x^{n}$. Suppose that $G$ is a subset of $S$ that forms a group. Then we know by the definition of a group that $G$ contains an identity element $1_{G}$, and thus the size of $G$ is at least $1$. Suppose, for contradiction, that the size of $G$ is strictly greater than $1$. Then there must exist another element $x \in G$ with $x \neq 1_{G}$. By the assumption on elements of $S$, there is an integer $n$ such that $x^{n+1} = x^{n}$, and this is an equation in $G$ since groups are closed under the group operation. In particular, $x^{n} \in G$, so there is an inverse $(x^{n})^{-1} \in G$ which we can multiply the above equation by to find $x = x^{n+1} \cdot (x^{n})^{-1} = x^{n} \cdot (x^{n})^{-1} = 1_{G}$, which contradicts our assumption that $x \neq 1_{G}$. Therefore, if $S$ is a finite semigroup satisfying property 2 above, then if there is any subset $G$ of $S$ which forms a group, it must necessarily be a group of size $1$.

Tags: Semigroups, groups

LQ8. Finite state machines and languages

A finite state machine $M$ consists of a finite set of states, each having two arrows leading out of it, labelled $0$ and $1$. Each arrow from state $x$ may lead to any state (both may lead to the same state, which might be $x$). One state is labelled the “initial” state; one or more states are labelled “accept”. The machine reads a finite binary string by starting at “initial” and considering each symbol in the string in turn, moving along the arrow with that label to the next state until the end of the string is reached. If the final state is labelled “accept”, the machine accepts the string. The language, $L(M)$ of the machine is the set of all the finite binary strings that the machine accepts.

  1. Design a machine whose language is all palindromic strings of length $6$ (i.e., strings for which the last $3$ symbols are a reflection of the first $3$).
  2. Suppose that $L(M)$ is not finite. Show that the number of strings in $L(M)$ of length $n$ or less grows linearly with $n$.
  3. Show that there is no machine such that $L(M)$ consists of all twice-repeated strings.

LQ8 Solution

For part 1, my initial idea was to imagine a finite state machine $M$ which could be visualized somewhat like a perfect binary tree of depth $7$ with a few adjustments. The initial state would be at the root of the tree, each branch would encode one of the $2^{6} = 64$ possible binary strings of length $6$, of which $2^3 = 8$ are palindromes, whose corresponding leaf nodes would be labelled “accept”. There would also need to be an additional “fail” node which acts as a sink node (leads to itself, not labelled “accept”) to account for strings of length greater than $6$.

This model can be refined to use fewer states, namely $1 + 2 + 4 + 8 + 8 + 8 + 8 + 1 = 40$: The first 4 layers are arranged as a binary tree to record the first three symbols in the string, then the next 3 layers check for the palindrome property, skipping to the fail state at layer 8 if symmetry is broken. The $8$ states in layer 7 are “accept” states where a palindrome of length $6$ has been recorded.

The graph of a finite state machine is a directed graph which will necessarily contain cycles. A sufficient condition for a finite state machine $M$ to have a language $L(M)$ of infinite size is to require that there is a cycle in $M$ containing an “accept” state. However this is not strictly required.

An example of a finite state machine $M$ for which its language $L(M)$ is not finite is when $M$ consists of only one state $s$, which is necessarily the initial state, but we also specify that $s$ is an accepting state. Then $L(M)$ consists of all binary strings of finite length (all strings are accepted). The number of strings in $L(M)$ of length $n$ or less is equal to the number of binary strings of length $n$ or less, which is $\sum_{k=0}^{n} 2^{k} = 2^{n+1} - 1$. This is not linear growth with $n$, but in fact exponential growth with $n$.

To show that there is no finite state machine $M$ such that its language $L(M)$ consists of all twice-repeated strings consider the following: Let $n > 0$ and let $w_{1}$, $w_{2}$ be two distinct binary strings of length $n$. Let $s(w_{1})$ and $s(w_{2})$ be the states in $M$ we reach if we follow the path from the initial state by reading $w_{1]$ and w_{2}$ respectively. Now consider the states in $M$ associated with reading the concatenated strings $w_{1} w_{1}$ and $w_{2} w_{1}$. By definition of the language $L(W)$ we know that $s(w_{1} w_{1})$ is an accepting state, whilst $s(w_{2} w_{1})$ is not an accepting state as $w_{2} w_{1}$ is a binary string of length $2n$ which cannot be expressed as a twice-repeated string (which would necessarily be of length $n$). Therefore $s(w_{1} w_{1}) \neq s(w_{2} w_{1})$. It follows that $s(w_{1}) \neq s(w_{2})$ because otherwise we could start at the same state $s(w_{1}) = s(w_{2})$ and move through the graph following the same path according to $w_{1}$, but end up at different states $s(w_{1} w_{1}) \neq s(w_{2} w_{1})$.

We have shown that for any $n > 0$, distinct words $w_{1}$, $w_{2}$ of length $n$ must each occupy distinct states $s(w_{1})$, $s(w_{2})$ in $M$,
since they are distinguished by $w_{1}$. As there are $2^{n}$ binary strings of length $n$, it follows that $M$ has at least $2^{n}$ states, but this applies for all $n > 0$ and there is no finite number which is greater than $2^{n}$ for all $n > 0$. Therefore there can be no finite state machine $M$ whose language $L(M)$ consists of all twice-repeated strings.

The above line of reasoning is closely related to the Myhill–Nerode theorem, which provides a necessary and sufficient condition for a language to be regular (that is, arising as the language associated to some finite state machine $M$).

References:

LQ9. Longest increasing subsequence of a permutation

Suppose $P$ is a permutation on $\{ 0, 1, \ldots, n − 1 \}$. We want to know the length of the longest monotonically increasing subsequence. That is, the largest $m$ such that there exist monotonically increasing $j_{1}, j_{2}, \ldots, j_{m}$ for which $P(j_{1}), P(j_{2}), \ldots, P(j_{m})$ are also monotonically increasing. Describe an algorithm that will determine $m$ using $O(n^{2})$ time and $O(n)$ memory.

LQ9 Solution

This question can be interpreted in terms of the Longest common subsequence problem between the sequences $(0, \ldots, n - 1)$ and $(P(0), \ldots, P(n - 1))$.

References:

Tags: Dynamic programming

LQ10. $541$ points in a unit circle

Given $541$ points in the interior of a circle of unit radius, show that there must be a subset of $10$ points whose diameter (the maximum distance between any pair of points) is less than $\frac{\sqrt{2}}{4}$.

LQ10 Solution

By the (generalised) Pigeonhole principle, it suffices to divide the interior of the unit circle into $60$ subsets each with diameter less than $\frac{\sqrt{2}}{4}$. Then, given $541$ points within the unit circle, there must be a subset out of these $60$ containing at least $10$ points.

It should be noted that the diameter of a square with side length $1$ has diameter equal to $\sqrt{2}$, the length of its diagonals (by Pythagoras’ theoreom). Therefore, a square with side length $\frac{1}{4}$ will have diameter $\frac{\sqrt{2}}{4}$. We will intersect such small squares with the interior of the unit circle to form our $60$ subsets.

Consider the unit circle circumscribed inside a square of side length $2$. We may divide this square into a grid of $64$ squares of side length $\frac{1}{4}$, which will necessarily cover the unit circle. In fact, we may remove the four small corner squares from the grid to obtain a set of $60$ small squares of side length $\frac{1}{4}$ which still cover the unit circle. This is because the four small corner squares lie completely at a distance at least $\sqrt{2} - \frac{\sqrt{2}}{4} = \frac{3 \sqrt{2}}{4} > 1$ from the center of the circle, and so do not intersect it at all.

References:

LQ11. Directed hypercube graph

Show how the edges of a cube ($8$ vertices; $12$ edges) can be directed so that some vertices have all edges pointing out (i.e., directed away from the vertex), and the remainder have one edge out and two in. Suppose the edges of a $5$-dimensional hypercube ($32$ vertices, $80$ edges) are directed so that all vertices have either $5$ edges pointing out, or $4$ edges in and $1$ out. Show that every $4$-dimensional subcube must contain precisely $6$ of the $5$-out vertices.